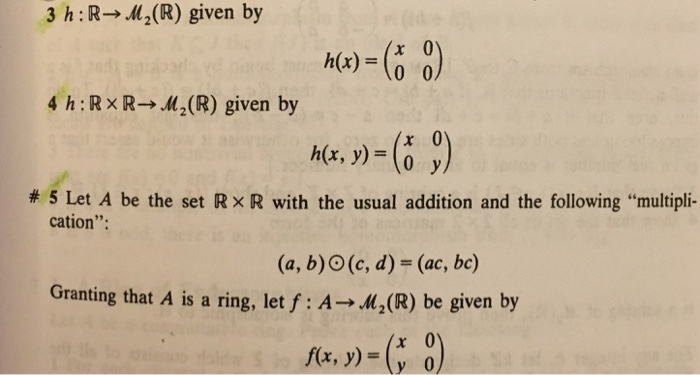Kernel of Ring Homomorphism - Definition - Homomorphism/ Isomorphism - Ring Theory - Algebra - YouTube
Solved Kernel of a homomorphism: 1. Find the kernel of the | Chegg.com
SOLVED:Let f : R divisor S be ring homomorphism and assume that S has no zero Check ALL that are correct The kernel of f is maximal ideal; R/Kerf is field if
An Algorithm to Calculate the Kernel of Certain Polynomial Ring Homomorphisms
abstract algebra - Why should the kernel of a ring homomorphism be an ideal? - Mathematics Stack Exchange
Group homomorphism - Wikipedia
Kernel of a Ring Homomorphism = {0} iff f is 1- 1- Homomorphism/Isomorphism - Ring Theory - Algebra - YouTube
Ring homomorphism - in ring theory, a branch of abstract algebra, a ring
abstract algebra - Relation between the kernel of two ring homomorphisms - Mathematics Stack Exchange
![Solved 1. Prove that 0 : Z[2] +Z15 defined by $(f(+)) = | Chegg.com](https://media.cheggcdn.com/media/f7d/f7dfc59f-b7c1-44f8-8910-dc2cbbf391bb/phpsvC4ts.png "Solved 1. Prove that 0 : Z[2] +Z15 defined by $(f(+)) = | Chegg.com")
Solved 1. Prove that 0 : Z[2] +Z15 defined by $(f(+)) = | Chegg.com
Ring homomorphism
Ring Kernel -- from Wolfram MathWorld
Solved The kernel of a ring homomorphism 0:R + R'is 1. {x | Chegg.com
![SOLVED:Let R be a ring and [, ] ideals of R with [ @ J Let JAIR{2 +I:ceJ} Show that J/[ is an ideal of the factor ring R}I Hint First recall](https://cdn.numerade.com/ask_images/5af9b15d86284f41b087a0697eeac839.jpg "SOLVED:Let R be a ring and [, ] ideals of R with [ @ J Let JAIR{2 +I:ceJ} Show that J/[ is an ideal of the factor ring R}I Hint First recall")
SOLVED:Let R be a ring and [, ] ideals of R with [ @ J Let JAIR{2 +I:ceJ} Show that J/[ is an ideal of the factor ring R}I Hint First recall
Solved The kernel of a ring homomorphism o: R R is 1. {r € | Chegg.com
SOLVED:Let 0 : R + R' be & homomorphism of rings (8 ) Prove that the kernel ker $ is an ideal of R. Prove that if N is an ideal of
Solved T F Let R be a ring with unity e (where e #0). Then | Chegg.com
RNT1.3. Ring Homomorphisms - YouTube
Chapter 6, Ideals and quotient rings Ideals. Finally we are ready to
🎯 Kernel Of Ring Homomorphism || Definition Of Ker (f) Definition of Kernel Of Ring Homomorphis 🎯 - YouTube
Ring homomorphism
abstract algebra - For a ring homomorphism, $\phi\left ( x \right )=0$ or $\phi\left ( x \right )=x.$ - Mathematics Stack Exchange
Solved E. Examples of Homomorphisms that each of the | Chegg.com
Homomorphism & Isomorphism of Rings | Kernel of Ring Homomorphism - YouTube
